The field content of the NMSSM is very similar to the MSSM; it differs merely by the addition of a singlet superfield S, which is introduced to address the μ-problem of the MSSM (for an exhaustive review of the NMSSM see e.g. [1]). The superpotential and soft supersymmetry-breaking terms of the Higgs sector are given by
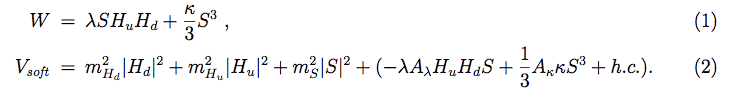 The phenomenology of this model can be easily connected to the simplified models that we have reviewed previously. If we disregard the Higgsinos and singlino (which if heavy are largely irrelevant for Higgs phenomenology) the Higgs sector of the NMSSM is essentially that of a Type II `2HDM + Scalar' model, where we can immediately identify Hd, Hu as H1,H2.
The phenomenology of this model can be easily connected to the simplified models that we have reviewed previously. If we disregard the Higgsinos and singlino (which if heavy are largely irrelevant for Higgs phenomenology) the Higgs sector of the NMSSM is essentially that of a Type II `2HDM + Scalar' model, where we can immediately identify Hd, Hu as H1,H2.
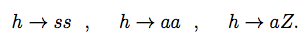 (3)
(3)
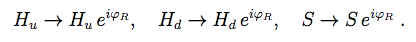 (4)
(4)
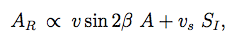 (5)
(5)
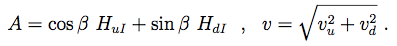
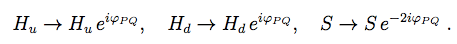 (6)
(6)
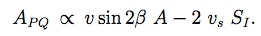 (7)
(7)
References
[1]U. Ellwanger, C. Hugonie, and A. M. Teixeira, The Next-to-Minimal Supersymmetric Standard Model, Phys.Rept. 496 (2010) 1-77, [arXiv:0910.1785].
[2]N. D. Christensen, T. Han, Z. Liu, and S. Su, Low-Mass Higgs Bosons in the NMSSM and Their LHC Implications, [arXiv:1303.2113].
[3]B. A. Dobrescu and K. T. Matchev, Light Axion Within the Next-to-Minimal Supersymmetric Standard Model, JHEP 0009 (2000) 031, [hep-ph/0008192].
[4]R. Dermisek and J. F. Gunion, The NMSSM Close to the R-symmetry Limit and Naturalness in h → aa Decays for m_a < 2m_b, Phys.Rev. D75 (2007) 075019, [hep-ph/0611142].
[5]D. E. Morrissey and A. Pierce, Modified Higgs Boson Phenomenology from Gauge or Gaugino Mediation in the NMSSM, Phys.Rev. D78 (2008) 075029, [arXiv:0807.2259].
[6]R. Peccei and H. R. Quinn, Constraints Imposed by CP Conservation in the Presence of Instantons, Phys.Rev. D16 (1977) 1791-1797.
[7]R. Peccei and H. R. Quinn, CP Conservation in the Presence of Instantons, Phys.Rev.Lett. 38 (1977) 1440-1443.
[8]E. Chun, Natural mu term with Peccei-Quinn symmetry, Phys.Lett. B348 (1995) 111-114, [hep-ph/9411290].
[9]P. Ciafaloni and A. Pomarol, Dynamical determination of the supersymmetric Higgs mass, Phys.Lett. B404 (1997) 83-88, [hep-ph/9702410].
[10]L. J. Hall and T. Watari, Electroweak supersymmetry with an approximate U(1)(PQ), Phys.Rev. D70 (2004) 115001, [hep-ph/0405109].
[11]B. Feldstein, L. J. Hall, and T. Watari, Simultaneous solutions of the strong CP and mu problems, Phys.Lett. B607 (2005) 155-164, [hep-ph/0411013].
[12]D. Miller and R. Nevzorov, The Peccei-Quinn axion in the next-to-minimal supersymmetric standard model, [hep-ph/0309143].
[13]R. Barbieri, L. J. Hall, A. Y. Papaioannou, D. Pappadopulo, and V. S. Rychkov, An Alternative NMSSM phenomenology with manifest perturbative unification, JHEP 0803 (2008) 005, [arXiv:0712.2903].
[14]O. Lebedev and S. Ramos-Sanchez, The NMSSM and String Theory, Phys.Lett. B684 (2010) 48-51, [arXiv:0912.0477].
[15]B. A. Dobrescu, G. L. Landsberg, and K. T. Matchev, Higgs boson decays to CP odd scalars at the Tevatron and beyond, Phys.Rev. D63 (2001) 075003, [ hep-ph/0005308].
[16]C. Panagiotakopoulos and K. Tamvakis, New minimal extension of MSSM, Phys. Lett. B 469 (1999) 145, [hep-ph/9908351].
File translated from TEX by TTH, version 4.03. On 15 Dec 2013, 22:46.